ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

АКТУАЛЬНОСТЬ ИССЛЕДОВАНИЯ. Одной из тенденций развития современного спорта является рост числа и популярности тех его видов, результаты которых выражаются относительными показателями эффективной деятельности спортсменов. Кроме того, ряд видов спорта с «абсолютными» показателями соревновательной деятельности из-за нестабильности условий ее проведения постепенно также переходят к относительным критериям успеха. Круг таких видов постоянно расширяется. Многие из них уже прошли точку пика своей популярности, а информационной основы их деятельности так и не создано. Спорт – это борьба за результат. Любая тема, проблема, теория в сфере спорта опирается на уровень результатов. Поэтому инструментарий спортивного достижения по отношению к ним занимает центральное место. Издержки инструментария предопределяют издержки эффективности государственной политики в области спорта, оптимальности управления им, любого научного исследования, подбора составов сборных команд, информационного стимула самосовершенствования спортсменов, обоснования оптимальных для поддержания здоровья нагрузок, другие социальные, экономические проблемы. Прогресс в этом направлении предопределяет прогресс в теории спорта. Сегодня теория спорта из-за отсутствия единого информационного пространства не может эффективно помочь рядовому тренеру. В каждом из множества аспектов его работы она формирует свои решения, никак не связанные с другими аспектами. Сегодня, как и столетие назад, определяющее положение в вопросах управления соревновательной и тренировочной деятельностью по-прежнему занимают экспертные тренерские оценки, основанные на части множества разнородных вторичных и третичных параметров (состав команды, режим замен, дозирование нагрузок, игровой опыт и т.п.). При этом большая часть этого множества оказалась вне зоны реального использования, что делает управление в таких видах спорта менее эффективным. Необходима информационная модель, позволяющая минимальным числом измеряемых универсальных первичных параметров управлять всеми остальными. Теория спорта остается теорией, если она не формирует модель информационного пространства, позволяющую практикам реально ее использовать единым программным обеспечением. Ключевую позицию среди первичных параметров занимает информационный массив рейтинга (рейтинг команды, игрока, базовых параметров игроков…). Попытки обособленного решения этой проблемы эмпирическим путем в каждом виде спорта пока не привели к необходимому универсальному решению. Обращение к данной теме обусловлено следующими ПРОТИВОРЕЧИЯМИ:

• между необходимостью научного обоснования государственной стратегии поддержки спорта и отсутствием объективной информации об эффективности ее реализации;
• между необходимостью научно обоснованных рекомендаций по определению состава сборных команд на международные соревнования и объективным информационным обеспечением таких решений;

• между необходимостью реализации принципа сознательности и активности в физическом воспитании, спортивной тренировке и недостаточной конкретизацией целевых установок в этой деятельности;
• между необходимостью количественного выражения показателей динамики разноплановых нагрузок при построении циклов многолетней спортивной подготовки и отсутствием механизма определения общего эквивалента разнообразной, разноплановой нагрузки;
• между необходимостью многоаспектного мониторинга спортивной подготовленности и сложностью его реализации в режиме постоянного использования.

ОБЪЕКТ исследования – информационная модель соревновательной деятельности в игровых видах спорта и единоборствах.

ПРЕДМЕТ исследования – информационно-кибернетическое управление соревновательным процессом.

ГИПОТЕЗА исследования:

Использование концепции рейтинга как результата макротурнира в информационной модели соревновательной деятельности игровых видов спорта и единоборств может позволить обеспечить преемственность решений на различных уровнях, в том числе:

1. Интерпретирование и прогнозирование итогов соревнований, определение рейтингов команд и составляющих ее игроков, эффекта тренировочной деятельности.

2. Сопоставление уровня игры спортсменов и постоянный контроль их подготовленности определением рейтинга либо из результатов официальных микроматчей, либо через полученные формы равномерного распределения составов команд при проведении личного первенства в командных видах спорта без изменения структуры игры.

3. Прогнозирование достижений спортсмена через установленную зависимость рейтинга от возраста.

4. Взаимодействие рейтинга спортсмена с его базовыми рейтингами по выделенным направлениям соревновательной деятельности, взаимодействие базовых рейтингов через линейную зависимость с параметрами соответствующих ключевых упражнений тренировочного процесса. Корректировка тренировочного процесса по оси рейтинг – базовый рейтинг – параметр ключевого упражнения обеспечит наиболее эффективное управление спортивной подготовкой за счет минимального числа однородных критериев.

5. Дозирование с наибольшей эффективностью соревновательной и тренировочной нагрузки соответственно в эквипараметрическом и эквидинамическом режимах.

6. Расширение сферы применения предлагаемой системы рейтинга в тех областях деятельности, где есть соревновательный момент и возможно выделение микроматчей участников.

ЦЕЛЬ ИССЛЕДОВАНИЯ - совершенствование преемственной взаимосвязи концепции рейтинга как результата кругового гипотетического макротурнира с параметрами тренировочной и соревновательной деятельности.

ЗАДАЧИ ИССЛЕДОВАНИЯ:

1. Концептуально обосновать содержание и принципы системы рейтинга, сформулировать условия корректной оценки результатов макротурнира.
2. Исследовать оптимальную форму проведения микротурниров личного первенства в командных видах спорта без изменения структуры игры.
3. Исследовать зависимость изменения рейтинга спортсмена от возраста.
4. Исследовать структуру игровых видов спорта, установить связь рейтинга с оценками соревновательной и тренировочной деятельности.
5. Обосновать режим наибольшей эффективности в распределении игровых и тренировочных нагрузок. Исследовать определение физиологического эквивалента частной нагрузки.
6. Обосновать применимость универсальной шкалы рейтинга в тех областях деятельности, где есть соревновательный момент.

ТЕОРЕТИКО-МЕТОДОЛОГИЧЕСКОЙ ОСНОВОЙ исследования были:

1. Работы, основанные на демократизации учебно-тренировочного процесса (Б.С. Гершунский (1974), Ю.Д. Железняк (1986), Ф. Конрад (1990), В.И. Андреев (2001)).

2. Общие положения теории спорта (Л.П. Матвеев (1991), В.М. Зациорский (1985), И.И. Алиханов (1991), Г.С. Туманян (1989), Ю.В. Верхошанский (1990), В.Н. Платонов (1982), О.П. Юшков (1995), В.К. Бальсевич (1985)).

3. Основные положения педагогического управления спортивной подготовкой (В.В. Лобановский (1981), А.В. Тарасов, (1976)).

4. Исследования по интерпретации полученных результатов в спорте (система «Атари-АТП» (1990), Г.П. Почекуев (1989), А.Л. Садовская (1981), Э. Эло (1963)).

5. Общие положения линейной алгебры и математической статистики (С.Д. Бешелев (1980), Б.А. Бондаренко (1968), Ф.Г. Гурвич (1984)).

7. Элементарные функции, графики, таблицы (Н.Ф. Гельфанд (1973), В.Д. Рыбасенко (1987)).

МЕТОДЫ исследования: теоретический анализ и обобщение научно-методической литературы, методы математической статистики и линейной алгебры, педагогические наблюдения, анкетный опрос, анализ игровой деятельности, педагогические эксперименты.

НАУЧНАЯ НОВИЗНА

1. Дано определение понятия «рейтинг» как результата годичного гипотетического кругового макротурнира. Сформулированы принципы, формирующие его структуру, условия корректного подведения итогов соревновательной деятельности: отсутствие изолированных микротурниров, исключение из рассмотрения результатов команд с разницей в рейтингах свыше 1000 пунктов и другие. Это позволяет минимизировать погрешность в подведении итогов существующих схем проведения соревнований, прогнозировать результаты несостоявшихся матчей.

2. Обоснованы оптимальные варианты составов участников микроматчей в микротурнире личного первенства командных видов спорта без изменения структуры игры и соответствующие им формулы пересчета результатов макротурнира, что позволяет спортсменам, постоянно контролируя уровень своей подготовки, повышать результативность тренировочного процесса.

3. Сформирован и использован в тренировочном процессе рейтинг-лист игроков. Совмещение на одном графике векторов изменения рейтинга от изменения возраста за период занятий спортсменов позволило установить вид зависимости рейтинга от возраста. Это совмещенные в оптимальном возрасте (22 – 25 лет) логистические функции восхождения и деградации рейтинга, которые позволяют прогнозировать результаты спортсменов.

4. В структуре игровых видов спорта выделены базовые компоненты игры: пас за спину, позитивный пас, обводка, отбор, верховые единоборства, восстановление, реализация голевых моментов, тактический эффект. Это позволило установить связь между соответствующими соотношениями выигранных и проигранных единоборств и рейтингами игрока по базовым компонентам. Подбор ключевых упражнений тренировочного процесса, параметры которых имеют линейную связь с соответствующим базовым рейтингом, позволяет эффективно корректировать тренировочный процесс с помощью как самого рейтинга, так и рейтинга по базовому компоненту.

5. Благодаря корректному определению объема спортивной нагрузки через использование физиологического эквивалента в различных компонентах игры обосновано ее наиболее эффективное эквипараметрическое и эквидинамическое распределение в рамках соответственно соревновательной и тренировочной деятельности.

6. Выделена соревновательная основа в процессе получения знаний учащимися, оценки научного творчества, что позволяет расширить область применения предлагаемой системы рейтинга.

ТЕОРЕТИЧЕСКАЯ ЗНАЧИМОСТЬ исследования заключается в формировании информационной модели, которая могла бы минимальным числом измеряемых первичных параметров (рейтинг, нагрузка, эффективность) позволить управлять всеми остальными; достижении на этой основе наибольшего эффекта управления; разработке основ системы рейтинга для широкой области применения.

ПРАКТИЧЕСКАЯ ЗНАЧИМОСТЬ заключается:

1) в корректном подведении итогов соревнований;

2) в освоении методики тренировок, ориентированной на рейтинг-лист в игровых видах спорта;

3) в программном обеспечении, контролирующем игровую деятельность и прогнозирующем дальнейшие результаты спортсменов, их команд;

4) в управлении подготовкой спортсменов минимальным числом однородных параметров;

5) в достижении наибольших командных результатов при соблюдении рационального распределения нагрузок в игровой и тренировочной деятельности, точности дозирования разноплановой нагрузки;

6) в расширении области применения системы рейтинга за счет тех областей деятельности, где есть соревновательный момент.

ОБОСНОВАННОСТЬ И ДОСТОВЕРНОСТЬ результатов исследований обусловлены системным анализом изучаемых явлений, использованием современных передовых концепций, методологических основ теории познания, корректной математической обработкой данных современными методами анализа, репрезентативностью исследуемого материала. Научные положения и практические рекомендации подтверждены результатами педагогических экспериментов.

АПРОБАЦИЯ И ВНЕДРЕНИЕ РЕЗУЛЬТАТОВ исследования. Результаты исследований использовались при подготовке национальной сборной, команд высшей лиги по мини-футболу «ВИЗ» и «Строитель», в рамках работы с командами 1 лиги по мини-футболу «Луч», «УПИ-2», «Торнадо» (все – Екатеринбург), «Три Богатыря» (Озерск, Челябинская область). Всего - 20 команд. Результаты использованы в практической работе со студентами кафедры игровых видов спорта ФФК УГТУ-УПИ (Екатеринбург), кафедры спорта ЮУрГУ (Челябинск). Автор провел 5 региональных и российских семинаров по проблеме рейтинга. Результаты докладывались на международных конференциях («Современные технологии и оздоровительные программы педагогического процесса по физической культуре и спорту в учебных заведениях», Белгород, 2002; «Оздоровительные технологии 21 века», Челябинск, 2002), вузовских конференциях, представлены в монографии, 10 публикациях в журнале «Теория и практика физической культуры».

ОСНОВНЫЕ ПОЛОЖЕНИЯ, ВЫНОСИМЫЕ НА ЗАЩИТУ:

1. Информационная модель из первичных параметров - рейтинг, нагрузка, эффективность - позволяет осуществлять полноценное управление соревновательной и тренировочной деятельностью спортсменов (режим замен, дозирование нагрузок, состав команды).
2. Обоснование понятия «рейтинг» как результата кругового гипотетического макротурнира и принципов, позволяющих реализовать данное определение, создает возможность обеспечить преемственность решений на различных уровнях.
3. Изучение закономерностей поведения рейтинга, устойчивость и универсальность получения его значений в различных проявлениях соревновательной и тренировочной деятельности (личное первенство, ключевые упражнения, возрастные корректировки и т.п.) позволяют находить через соответственно эквипараметрический и эквидинамический режимы дозирования нагрузок максимальный уровень результатов.
4. Уровень игры равен сумме рейтинга участника и эффективности его применения, которая зависит от выбранной тактики - способов эквипараметрического распределения матчевой нагрузки в пользу больших значений базовых рейтингов партнеров на позиции наиболее низких базовых рейтингов противостоящего соперника

СТРУКТУРА ДИССЕРТАЦИИ. Диссертация состоит из введения, пяти глав, выводов, списка литературы и приложений. Работа изложена на 304 страницах машинописного текста, включает 14 педагогических экспериментов, 17 таблиц, 84 формулы, 2 математических доказательства, 19 рисунков, 10 диаграмм, программы для персонального компьютера. Список литературы включает в себя 243 работы, в том числе 30 работ иностранных авторов.

ОСНОВНОЕ СОДЕРЖАНИЕ ДИССЕРТАЦИИ

В работе использовались следующие термины:

Базовые (частные) рейтинги – рейтинги, соответствующие видам единоборств соревновательной деятельности.

Игровые виды спорта (ИВС) - командные виды спорта, в которых задействован мяч и существует распределение по амплуа.

Истинное значение рейтинга – значение рейтинга спортсмена при нулевой соревновательной нагрузке.

Изолированный микротурнир (ИМ) - турнир, в котором принимает участие меньшая часть соревнующихся участников, не имеющая официальных встреч с оставшимся большинством. Участникам изолированного микротурнира не может быть присвоен рейтинг. Он корректируется только на основании результатов микротурнира, участники которого имеют официальные встречи с оставшимся большинством.

Контрольная игра - альтернативное название личного первенства в ИВС.

Личное первенство – форма двусторонней игры в ИВС, при которой составы обеих команд меняются так, чтобы каждый игрок сыграл с каждым одинаковое количество микроматчей.

Система рейтинга – построение теории рейтинга, обеспечивающее в рамках макротурнира преемственную взаимосвязь среди параметров соревновательной и тренировочной деятельности.

Макротурнир - любой турнир с произвольной формой его проведения среди всех участников, в котором отсутствуют изолированные микротурниры.

Микроматч - минимальный отрезок игры в командных видах спорта, который проходит без изменения составов команд.

Параметр - числовой критерий ключевого упражнения, находящийся в линейной зависимости от соответствующего ему базового рейтинга. Ключевое упражнение может быть разложено по фазам выполнения на сумму других упражнений. Такие упражнения, обладающие линейной связью с ключевым упражнением, назовем подводящими.

Первичный параметр – имеющий достоверную корреляционную связь со всеми параметрами в информационном массиве. Вторичные, третичные – имеющие корреляционную связь с частью других параметров того же массива.

Рейтинг - смещенный в область целых положительных чисел результат участника всеобщего гипотетического кругового годичного макротурнира.

Факторная компенсация - количество пунктов, на которое изменяется рейтинг участника под воздействием данного фактора.

Физиологический коэффициент – это числовой эквивалент относительной энергетической стоимости для организма каждого единоборства того или иного базового компонента.

Эквипараметрический режим - распределение нагрузки официального матча среди базовых компонентов игроков, при котором более высокие частные рейтинги под воздействием возрастающей нагрузки снижаются до повысившихся от сокращения нагрузки меньших частных рейтингов.

На сегодняшний день рейтинг представляет собой разобщенные по различным уровням и сферам знания «формулы успеха» с набором вторичных, нелинейно взаимодействующих между собой параметров, не имеющих взаимной преемственности. Обычно это уравнение линейной множественной регрессии с математическим подбором оптимальных коэффициентов или «формула успеха», где коэффициенты подбираются группой экспертов и не корректируются реальной ситуацией. Поэтому рейтинг чаще всего представляет собой некую массу информации без обратной связи с результатами игр. Основной причиной узости диапазона возможностей таких рейтингов являются нелинейный характер взаимодействия между собой слагаемых величин и, как следствие, непредсказуемое поведение рейтинга.

Предполагается, что замена наиболее цитируемой концепции по ниже перечисленным проблемам на концепцию, предлагаемую соискателем, может быть обоснована новыми возможностями:

1. Замена информационной модели из всей совокупности параметров на модель из первичных параметров - рейтинг, нагрузка, эффективность - позволяет осуществлять более эффективное управление соревновательной и тренировочной деятельностью спортсменов (режим замен, дозирование нагрузок, состав команды и т.п.).

2. Замена концепции рейтинга как суммы произведения выделенных параметров деятельности и подобранного экспертами удельного веса на концепцию рейтинга как результата макротурнира позволяет выявить необходимые регламентирующие его принципы, прогнозировать итоги соревнований.

3. Замена выборочного использования отдельных принципов формирования той или иной шкалы рейтинга на его полное применение позволяет создать универсальную систему, поглощающую действующие классификации как частный случай.

4. Замена концепции, по которой погрешность определения официальных результатов соревнований определяется издержками принципа начисления очков, схемой турнира и является составной частью его итогов, на концепцию соответствия порядка проведения соревнований адекватному распределению итоговых мест позволяет сформулировать условия корректности результатов макротурнира, классифицировать наибольшее число участников за минимальное число туров на основе рейтинг-формулы.

5. Замена экспертного определения компенсации различных факторов в итоговой оценке или его нивелирование условиями соревнований (например, «свое» - «чужое» поле) на выявленное отклонение результатов под воздействием этих факторов может позволить получить итоги макротурнира, нивелированные по всем этим неравным условиям.

6. Замена концепции оценки игровой деятельности игрока по совокупности вторичных параметров на концепцию определения его рейтинга решением системы линейных уравнений по балансу забитых и пропущенных мячей микроматчей с участием этого игрока позволяет корректировать ход игры, сравнивать всех игроков макротурнира, определять состав сборных команд.

7. Создаваемую игроком разность забитых и пропущенных мячей можно определить с помощью личного первенства в командных видах спорта без изменения структуры игры, которое наиболее удобно проводить в виде серии круговых микротурниров с равномерным распределением как партнеров, так и соперников. Это позволяет постоянно контролировать подготовленность спортсменов, проводить «турниры звезд» в каждом виде спорта.

8. На основе сравнения результатов участника макротурнира в разные периоды могут быть получены «вторичные» шкалы. Замена концепции оценки предлагаемых методик уровнем результатов на концепцию оценки любых методик по среднему приросту уровня результатов использующих ее игроков по сравнению с игроками, тренирующимися через двусторонние игры, может позволить создать соответствующую шкалу методик.

9. Замена эмпирических оценок возрастной эволюции ряда спортивных качеств на график совмещенных логистических зависимостей рейтинга от возраста позволяет прогнозировать возможности спортсмена, компенсировать в итоговой оценке фактор возраста за счет экстраполяции результатов на один возраст, расширить социальную базу спорта за счет компенсации ряда факторов вариативным изменением правил.

10. Выявление силовых линий точек игрового поля с равной вероятностью поражения цели позволяет по приросту такой вероятности оценивать любое действие, выявить виды технико-тактических единоборств: отбор, обводка, позитивный пас, пас за спину, верховые единоборства, (атакующие, оборонительные; с восстановлением, без восстановления), реализация голевых моментов.

11. Замена концепции оценки уровня игрока уровнем его команды на концепцию оценки выигранных и проигранных игроком выделенных технико-тактических единоборств по приросту вероятности забить мяч, сложению этих приростов в разность забитых и пропущенных мячей игроков, в итоговую командную разность позволяет связать частные рейтинги игрока по базовым компонентам игры с рейтингом игрока, команды.

12. Замена концепции распределения нагрузок среди игроков пропорционально уровню их игры на концепцию эквипараметрического распределения обеспечивает достижение наибольшего уровня результатов соревновательной деятельности.

13. Замена концепции структурирования тренировочного процесса микро -, мезоциклами на концепцию «суперкомпенсационных» «волн» разного уровня позволяет упростить контроль и точнее дозировать тренировочные нагрузки.

14. Замена концепции универсального в данном виде спорта распределения тренировочных нагрузок среди базовых компонентов игры на концепцию эквидинамического режима дозирования при компенсации фактора «суперкомпенсационных» «волн» разного уровня может позволить обеспечить наибольшие темпы прироста результатов игроков за счет корректировки индивидуальных тренировочных графиков результатами микротестов.

15. Замена концепции эмпирических числовых ориентиров тренировочного процесса, выраженных в метрах, секундах, числе попыток, другими величинами на концепцию линейной взаимосвязи «относительного» частного рейтинга игрока с «абсолютным» параметром ключевого упражнения может позволить контролировать тренировочные достижения в рамках макротурнира.

16. Замена совокупности аналитических зависимостей в каждом аспекте соревновательной и тренировочной деятельности единым балансовым уравнением может позволить осуществить взаимосвязь этих аспектов и упростить производимые расчеты, обеспечит эффективное управление спортивной подготовкой за счет минимального числа однородных критериев.

17. Замена концепции тактики игры как совокупности средств, способов и форм ведения спортивной борьбы на концепцию тактики как эквипараметрического распределения матчевой нагрузки в пользу больших значений базовых рейтингов партнеров на позиции наиболее низких базовых рейтингов соперников позволяет оценивать уровень игры по сумме рейтинга участника и эффективности его применения; оценивать «сыгранность» данного игрока с партнерами; управлять игрой через выгодные «непропорциональные» размены в атаке и «пропорциональные» размены в обороне.

18. Замена концепции здоровья как степени адаптации к условиям окружающей среды на концепцию здоровья как наибольшего значения произведения всего объема разноплановой повседневной нагрузки на уровень ее выполнения позволяет определять стоимость любой нагрузки для организма через физиологические коэффициенты и точно дозировать нагрузку, удерживая ее в точке наибольшего благоприятствования.

19. Замена концепции достижения гармоничного физического развития через общеразвивающие упражнения до выполнения соответствующих норм ГТО на концепцию выбора минимального круга видов спорта с наибольшим переносом уровня результатов на все остальные может позволить повысить уровень гармоничного развития за счет большей эмоциональной значимости для занимающихся, создать базу для смены спортивных увлечений с возрастом.

20. Замена концепции экспертных оценок уровня знаний учащихся на концепцию парного «конкурса знаний» в рамках макротурнира может позволить ориентировать образовательный процесс на способность учащихся активно пользоваться полученными знаниями.

21. Замена концепции произвольного выбора параметров системы рейтинга для каждой области применения на концепцию выделения первичных конфликтующих параметров противостояния может позволить использовать универсальную систему рейтинга в других областях деятельности человека.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СИСТЕМЫ РЕЙТИНГА

КОНЦЕПТУАЛЬНАЯ ОСНОВА ПОСТРОЕНИЯ СИСТЕМЫ РЕЙТИНГА

Назовем рейтингом смещенный в область целых положительных чисел результат участника всеобщего гипотетического кругового годичного макротурнира. Рассмотренные в Главе 2 принципы дают возможность реализовать это определение.

1. Приоритет гола над очком. Информационной основой рейтинга являются первичные параметры игровой деятельности в виде забитых (З) и пропущенных (П) мячей, голов, количества реализованных действий и т.п..

2. Выбор вида функциональной зависимости. Выбранная функция должна:

2.1. Обладать свойством антикоммутативности: F (З,П) = - F (П,З).

2.2. Работать в избранном числовом интервале, а не по всей шкале.

2.3. Не выходить за пределы четырех действий арифметики и обеспечить минимальное число арифметических действий при пересчете рейтинга.

2.4. Свести к минимуму суммарную разницу между результатами участников в личной встрече и их общими результатами. Отсутствие этого принципа ведет к неустойчивому поведению рейтинга.

3. Принцип транзитивности утверждает, что если участник А предпочтительнее участника Б по совокупности результатов, а Б аналогично предпочтительнее С также по всей совокупности зафиксированных в течение года результатов, то уровень А выше, чем уровень С. Он позволяет провести макротурнир без обязательной встречи каждого с каждым. Тем самым создается возможность превратить круговой макротурнир в гипотетический, когда можно играть не все игры. Уровень игры, определенный на основе полученной части результатов, экстраполируют на всю сумму игр. Отсутствие этого принципа означает требование встречи каждого участника макротурнира со всеми остальными, что не имеет перспективы.

4. Принцип трансляции в глубину призван обеспечить неизменность, преемственность способа пересчета рейтинга при переходе с макроуровня на последующие нижележащие слои, от уровня команд на уровень составляющих ее игроков, от уровня игроков - на уровень их базовых компонентов игры, и наоборот. Он предполагает возможность замены нескольких соперников одним, им эквивалентным. Отказ от этого принципа приводит к потере взаимодействия между различными уровнями.

5. Принцип асимптотической устойчивости результатов означает возможность получения единственного решения в распределении рейтингов, исходя из полученных результатов независимо от их исходных значений. Наиболее удобным способом реализации этого принципа является составление и последующее решение соответствующей системы линейных уравнений (далее СЛУ). При неравном нулю определителе СЛУ всегда имеет единственное решение. Отсутствие этого принципа приводит к существованию множества решений при одних и тех же результатах макротурнира, что равносильно отсутствию решения как такового.

6. Средний рейтинг макротурнира задается таким, чтобы рейтинг самого слабого из участников был величиной положительной. Прогресс множества различных участников не бывает синхронным. Средний рейтинг макротурнира корректируется по изменению средней плотности расположения участников на шкале рейтинга, которая возрастает по логистическому типу зависимости на начальном этапе развития вида спорта. Каждому новому участнику присваивается рейтинг, равный среднему рейтингу макротурнира.

7. Факторная компенсация. Существуют факторы (m), влияющие на итоговый результат и создающие неравные условия для участников. Выявление значения любого фактора предполагает сравнение результатов участника до и после его воздействия при нивелировании всех остальных. Компенсация суммы таких независимых, невзаимодействующих факторов должна быть равна сумме их компенсаций. Тогда официальным итогом соревнований будет сумма фактического рейтинга i-го участника и величины компенсаций различных факторов (чужое поле, климат, пол, возраст…):

Rтiофиц = Rтi + . (1)

ОПТИМИЗАЦИЯ ПАРАМЕТРОВ СИСТЕМЫ РЕЙТИНГА:

Выбор вида зависимости. Назовем процентом детерминации (ПД):

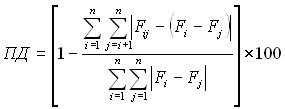. (2)

Используем таблицу кругового микротурнира в качестве модели этого макротурнира. Сопоставим результаты в личных встречах и показатели общей результативности в трех видах спорта с различной результативностью.

Подбор функций осуществлялся на основе справочника (Рыбасенко В.Д. и др., 1986); перебором ранее предложенных функций; перебором возможных вариантов наиболее простых конструкций функций через чередование знаков скобок, арифметических действий и забитых (З), пропущенных (П) мячей; пересмотром всех вариантов разложения в ряд элементарных функций. Данные по некоторым видам зависимости приведены в таблице 1. В соответствии с пунктами 2.1-2.4 выберем вид функциональной зависимости и обозначим как :

. (3)

Коэффициент 1000 задает масштаб шкалы рейтинга. Если после решения СЛУ в исходных данных найдены результаты встреч соперников с разницей в полученных рейтингах более 1000 пунктов, то их следует исключить и решить СЛУ заново.

Таблица 1

Процент детерминации для некоторых функций.

Вид функции	Мини-футбол		Хоккей	Футбол
	Чемпионат России 1993 г. 3 таблицы по 6 команд в 3 круга	Чемпионат мира 1994 г. 6 таблиц по 4 команды в 1 круг	Чемпионат России 1993 г. 1 таблица 12 команд в 3 круга	Чемпионат СССР 1990 г. 1 таблица 12 команд в 3 круга	Чемпионат России 1993 г. 1 таблица 18 команд в 2 круга
(З-П)/(З+П) Таблица Эло Ln (З/П) (З/П)-(П/З) З-П З2 - П2 (1/П)-(1/З) З/П	70.09 70.71 70.71 63.64 58.04 16.52 3.55 3.55 -78.17	38.34 37.35 37.35 39.62 32.18 25.69 9.88 3.77 -35.53	35.13 29.74 29.74 36.89 2.09 8.02 0.44 -36705 -130.05	18.75 9.28 9.28 27.94 -21.59 5.69 0.44 -29983 -145.58	-10.46 -15.206 -15.206 -3.45 -30.08 4.14 0.35 -12610 -120.04

Трансляция в глубину для найденного вида зависимости. Разность, полученная командой в ходе турнира, накапливается из разностей в текущих n играх:

З - П = З1-П1 +... + Зn-Пn ;

;

;

. (4)

При этом . Величина i = (Зi+Пi)/(З+П) – доля участия данного результата в общей оценке. По определению рейтинг - число положительное. Поэтому необходимо смещение вверх по числовой шкале на такую величину, при которой рейтинг самого слабого из участников будет величиной положительной:

.

;

.

Аналогично рейтинг команды раскладывается на рейтинги ее игроков. Так, при переходе на каждый следующий слой форма пересчета сохраняется.

Формирование системы линейных уравнений макротурнира. Рассмотрим полностью заполненную таблицу любого произвольного микротурнира.

1 -12 -13.. -1(n-1) -1n

-21 1 -23 … -2(n-1) -2n

………………………………

-(n-1) 1 -(n-1) 2 -(n-1) 3… 1 -(n-1) n

Таким образом, общий вид СЛУ таков:

…………………….. (5)

Зачеркнем любую строку, будем считать ее неизвестной. Потерянную информацию можно восстановить по соответствующему столбцу. Это означает, что СЛУ, соответствующая всей таблице, имеет множество решений. Чтобы СЛУ имела единственное решение, необходимо либо заменить в ней любое уравнение некоторым другим, либо просто добавить это уравнение к уже имеющимся. На практике предпочтительнее использовать (n+1) уравнение, определяющее средний рейтинг данного турнира через рейтинги всех (или части) его участников: . Есть только одно решение СЛУ, полученной после добавления данного (n+1) уравнения к существующим n. Доказательство приведено в тексте диссертации.

Оптимизация пересчета рейтинга. Разобьем макротурнир на два произвольных микротурнира. Найдем из соответствующих им СЛУ рейтинги участников и объединим результаты на основе принципа трансляции в глубину:

Rt i = i1Rti1 + i2Rti2.

В тексте диссертации математически доказано, что решения, полученные через решение СЛУ по микротурнирам и объединенные на основе принципа трансляции в глубину, эквивалентны общему решению СЛУ по всему макротурниру.

В некоторых видах спорта результативность фиксирована. Например, в шахматах: 1:0; 0,5:0,5; 0:1. Если все значения в СЛУ будут равны (равномерное распределение), то можно получить решения по макротурниру вообще без решения СЛУ. Тогда можно просто подставить (n+1) уравнение во все остальные и тривиально, прямым сложением среднего рейтинга турнира и величины i получить результат конкретного участника. Пусть есть j микротурниров с решением соответствующей СЛУ по i-му игроку в виде Rtij и есть новый j+1 микротурнир с решением Rti(j+1). Таким образом, задача, ранее считавшаяся «типично нелинейной», стала линейной и допускает тривиальное решение СЛУ (5) в виде уравнения (6), подобного уравнению Эло.

Rt i = ( ijRtij + i(j+1)Rti(j+1) )/( i(j+1) + ij) =

= Rtij + ( i(j+1) /( i(j+1) + ij)) ( Rti(j+1) - Rtij). (6)

ВОЗМОЖНЫЕ ВАРИАНТЫ ПРОВЕДЕНИЯ МАКРОТУРНИРА

Во многих ИВС результат игры складывается не напрямую из баланса забитых (З) и пропущенных (П) мячей, а по совокупности сетов, геймов, партий и т.п. Такая мера помогает искусственно повысить плотность результатов и зрелищность игр. Девальвация фактических результатов не позволяет определить соотношение сил точнее, провести макротурнир за год из-за необходимости восполнения утраченной информации большим числом игр. Поэтому при проведении макротурнира так же ориентируемся на забитые (З) и пропущенные (П) мячи.

Возьмем результаты любого кругового турнира и произвольно исключим некоторую их часть, с таким расчетом, чтобы обозначилась та или иная формула. Оценим степень сходимости результатов кругового макротурнира с результатами на основе выбранной формулы.

Олимпийская формула. Отметим очень широкий диапазон сходимости результатов в зависимости от случайности выбора – от 40 до 60 %. К последней отметке (60 %) он подходил в случаях относительно равномерного рассеивания сильнейших команд.

Смешанная (зонально-олимпийская) формула. Процент соответствия колебался в интервале 70-90 %. Среднее значение составило 82 %.

Круговая формула. Круговую формулу по определению считаем 100 %, хотя более правильно говорить о 95 % из-за погрешности очковой схемы интерпретации.

Швейцарская система и рейтинг-формула.

Рейтинг-формула. На старте макротурнира всем участникам присваивается одинаковый средний рейтинг. После каждого тура следующее значение рейтинга получают как средневзвешенное, пропорциональное результативности. Для того чтобы определить границы микротурнира, произвольно выбирается участник, выписывается круг его соперников, затем выписываются те, с кем они играли, и так далее. Получаем список данного изолированного микротурнира (ИМ). Затем из числа оставшихся участников произвольно выбираем одного и аналогично выясняем круг его ИМ. Каждому участнику назначается наиболее близкий по текущему рейтингу соперник из выбранного противоположного ИМ. При этом происходит полное слияние двух ИМ в один, большей размерности. Если количество участников в таких ИМ неодинаково, то кто-то из них останется без соперника. Его рейтинг по окончании тура изменяется настолько же, насколько в среднем изменился рейтинг всех остальных, играющих в туре его партнеров по ИМ. Турнир завершается слиянием всех ИМ в макротурнир. Полученный в последнем туре рейтинг соответствует двум последним результатам. Чтобы не потерять другие, более ранние достижения, их заново пересчитывают и усредняют по всей сумме результатов (6). Оптимальное число соревнующихся N при числе туров к равно 2К. Рейтинг-формула соблюдает равномерность связей, интервал в 1000 пунктов, учитывает результативность встреч.

Достижения обеих систем оказались близкими к отметке 95 %. Это связано с аналогичностью схемы их действия. Однако если в случае со швейцарской системой данный процент можно считать естественной погрешностью, то у рейтинг-формулы другой характер отклонения. Для интерпретации результатов используются очки – грубая упрощенная форма рейтинга.

Вопрос о формуле турнира – это чисто расчетный вопрос, который более правильно решать из определения рейтингов участников, их результативности из предыдущих достижений и предположительного расчета сходимости предлагаемой формулы. Она должна изменяться при изменении соотношения сил, плотности результатов, чтобы гарантировать участникам 100% справедливость в распределении мест.

УСЛОВИЯ КОРРЕКТНОСТИ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ МАКРОТУРНИРА:

1. Отсутствие изолированных микротурниров.
2. Исключение из рассмотрения результатов с разницей Rti – Rtj 1000.
3. Макротурнир продолжается до момента стабилизации средней плотности результатов

k+1, k, (7)

где к – число туров. Первые туры дают некорректную оценку, которая затем стабилизируется через число туров, большее, чем k (n )/( n 2), где – число участников. При этом следует отметить разницу. В случае решения через СЛУ плотность результатов в начале из-за минимального числа данных в первых турах достигает максимального значения и потом сокращается. Если определение рейтинга идет по упрощенной формуле, то знак в равенстве меняется на противоположный, поскольку в этом случае всем соревнующимся на старте присваивается равный рейтинг. И только по прошествии какого-то числа игр участники расходятся по полюсам шкалы рейтинга. Поэтому равенство k k+1 отражает момент, когда стартовое значение перестает играть нивелирующую роль.

4. Погрешность определения рейтинга участника 2000 (З+П) должна быть меньше среднего интервала их расположения

2000 (З+П) <. (8)

5. Результаты округляются до значений, соответствующих плотности.

Назначение игр в рамках макротурнира. Будем рассматривать каждую пару участников, находящихся друг от друга на расстоянии не более чем 1000 пунктов. Эта пара может быть связана друг с другом некоторым числом n(i) личных встреч (А-Б, i=1), через встречи с третьими участниками (А – С – Б, i=2), через встречи с третьими и четвертыми участниками (А – С – Е – Б, i=3). Тогда коэффициент их взаимосвязи К может быть представлен как:

. (9)

Коэффициент К может характеризовать полуизолированные турниры, способствует их выявлению, снижению искажений структуры макротурнира.

Физическим смыслом рейтинга данного участника можно считать усредненную по всей совокупности игр текущую или итоговую сезонную оценку его результатов, экстраполируемых на весь макротурнир. Разница рейтингов указывает на результат матча (или серии матчей), если известна его общая результативность, которая может быть определена. Ожидаемый результат встречи соответствует всей сумме результатов ранее сыгранных матчей. Рейтинг i-го игрока соответствует рейтингу команды, состоящей только из i-х игроков.

ПРОГНОЗИРОВАНИЕ РЕЗУЛЬТАТОВ МАТЧЕЙ. Данная тема была рассмотрена на примере прошедшего в Голландии и Бельгии чемпионата Европы по футболу 2000 года. После того как были определены рейтинги участников, можно было бы сразу определить результаты их личных встреч:

Rti – Rtj = = (З - П) 1000 / (З + П). (10)

Для этого можно было бы подставить на место (З + П) среднюю результативность всех встреч (2,75). Однако более правильно составить еще одну СЛУ с участием результативности (Рез) участников:

Ni Рез i + Рез j = (Зi + Пi), (11)

где Ni – число матчей, сыгранное i-м участником; (Зi + Пi) – сумма забитых и пропущенных им мячей во всех матчах; j – все соперники i на данном турнире. Полученные значения результативности (Рез i + Рез j) следует подставить в (10) вместо (З + П). Тогда прогноз встречи будет учитывать результативность обеих команд. Полученные прогнозы соответствуют среднему уровню выступления команд и всегда вариативно отличаются от конкретных итогов. Они приведены в тексте диссертации. Предполагаемые итоги турнира были определены из той логики, что чемпион – 1, проигравший в финале – 2 и так далее. Примем результаты полученного кругового макротурнира как эталонные и оценим их среднее значение отклонения от официальных итогов. Оно равно 2,6 места. При 15 участниках такая погрешность (далее - сходимость) составляет 83 %. Это не очень много для рокировок в глубине турнирной таблицы, но на уровне фаворитов турнира воспринимается весьма болезненно. Вопрос о формуле турнира – это вопрос, который более правильно решать из определения рейтингов участников и их результативности из предыдущих достижений и предположительного расчета сходимости предлагаемой формулы. Она должна изменяться при изменении соотношения сил, плотности результатов. Минимальное число матчей предлагаемой формулы должно быть таким, чтобы гарантировать участникам справедливое распределение мест.

В качестве еще одного ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА приведены рейтинги участников всех прошедших чемпионатов мира по футболу.

КОРРЕКТИРОВКА ПОДГОТОВКИ СПОРТСМЕНА

НА ОСНОВЕ ЕГО РЕЙТИНГА В МАКРОТУРНИРЕ

Результатом игры в командных видах спорта является разность забитых и пропущенных мячей. Она складывается в ходе матча из разностей отдельных игроков. Однако оценить приносимую игроком разность, «увидеть» ее в обычной игре невозможно из-за того, что партнеры и соперники могут «экранировать» его фактический уровень. Не выравнивая фактор игровой среды (партнеры, соперники), эту разность можно только вычислить. Для этого следует выписать состав и результаты микроматчей, в ходе которых не было замен. Такие равенства формируют СЛУ. Полученный из нее рейтинг игрока по сравнению со средним рейтингом макротурнира, по сути дела, пропорционален создаваемой им разности в противостоянии со всеми остальными участниками.

=

(12)

Однако эти результаты будут приблизительными из-за неопределенности в распределении фактической нагрузки внутри микроматча. В общем случае можно принять эту нагрузку равной (0,2). Более правильно ее корректировать с градиентом ±0,04 на каждые 100 пунктов отклонения рейтинга от среднего по команде значения. В этом случае решать СЛУ приходится дважды. Вопрос о вычислении фактических значений будет рассмотрен в следующей главе.

Возможна такая форма игры, при которой можно «увидеть» создаваемую игроком разность. Предположим, что есть некоторое (n) количество игроков с неизвестными рейтингами Rti и некоторая сумма микроматчей, в которых одни и те же игроки были то партнерами, то соперниками.

, где i = 1,…., N;

(13)

Для любого микротурнира игроков («контрольной игры») можно получить соответствующую СЛУ («общее решение») (13). Главные требования в личном первенстве - это привычный для игрока игровой режим на привычной позиции при отсутствии изолированных микротурниров. Однако при произвольном режиме их очень трудно выполнить. Поэтому предлагается такой вариант проведения личного первенства, при котором распределение равномерно как по партнерам, так и по соперникам. Это позволяет тривиально решать СЛУ микротурнира, придать ему необходимую организационную форму, получить привычную ритмичность игры, играть на привычной позиции. Тогда

Rti = Rtсредн + . (14)

Чтобы найти оптимальное распределение, сначала рассчитаем минимальное количество микроматчей. Для этого принимаем число участников равным минимуму, при котором можно проводить двустороннюю игру. Затем определяем минимальное целое количество циклов, при котором все игроки могут быть партнерами и аналогично - соперниками. Далее ищем число микроматчей, при котором они сходятся. Для распределения 22 число игр равно трем. В мини-футболе минимальное число участников с обеих сторон - восемь. При распределении четыре на четыре i-й игрок играет с каждым из партнеров равное количество игр. Минимальное их число равно 2.33. Например, в первом микроматче 1 играет со 2,3,4, во втором - с 5, 6 и 7, а на третий остается только один восьмой игрок. Значит, минимальное целое число игр равно семи – 2.33 3 = 7. Могут ли в такое же число игр уложиться соперники? Их минимальное число игр равно 1.75. Например, в первом микроматче соперниками 1-го игрока могут быть игроки 2,3,4,5, во втором - 6,7 и 8. Баланс равен: 2.33 3= 7 =1.75 4. Ожидаемое число микроматчей при распределении 44 равно семи. С каждым из партнеров i-й игрок играет 3 раза, а против него - 4. После определения минимального числа микроматчей последовательно распределяем по ним следующего i-го игрока, так, чтобы его распределение с предыдущими i-1 игроками было равномерно как в качестве партнера, так и в качестве соперника. Для этого используем диаграммы, на которых в ходе заполнения позиций по микроматчам отмечаем количество игр i-го игрока с каждым из 1,..,i-1 партнером и каждым 1,..,i-1 соперником, стараясь каждым следующим заполнением приблизить его к равномерному.

Для 22: 1. 12/34 2.13/24 3. 14/23 Rti = Rtсред + 1.5 . (15)

(3Rt(1)+ Rt(2)+ Rt(3)+ Rt(4))/6 - (2 Rt(2)+2 Rt(3)+2 Rt (4))/6 =

8 7
							***
6						***	***
5					***	***	***
4				***	***	***	***
3			***	***	***	***	***
2		***	***	***	***	***	***
	***	***	***	***	***	***	***

1 2 3 4 5 6 7 8

Диаграмма 1. Число игр с каждым партнером (4 на 4)

Для 44: Rti = Rtсред + 3.5 . (16)

1. 1234/5678 2. 1256/3478 3. 1278/3456 4. 1357/2468

5. 1368/2457 6. 1458/2367 7. 1467/2358

Для 55: Rti = Rtсред + 4.5 (17)

1. 1 2 3 4 5 / 6 7 8 9 10 7. 1 2 5 7 10 / 3 4 6 8 9 13. 1 3 8 9 10 / 2 4 5 6 7

2. 1 2 3 6 8 / 4 5 7 9 10 8. 1 2 8 9 10 / 3 4 5 6 7 14. 1 4 5 8 9 / 2 3 6 7 10

3. 1 2 3 7 9 / 4 5 6 8 10 9. 1 3 5 7 8 / 2 4 6 9 10 15. 1 4 6 7 8 / 2 3 5 9 10

4. 1 2 4 7 8 / 3 5 6 9 10 10. 1 3 4 6 9 / 2 5 7 8 10 16. 1 4 7 9 10 / 2 3 5 6 8

5. 1 2 4 6 10 / 3 5 7 8 9 11. 1 3 4 5 10 / 2 6 7 8 9 17. 1 5 6 7 9 / 2 3 4 8 10

6. 1 2 5 6 9 / 3 4 7 8 10 12. 1 3 6 7 10 / 2 4 5 8 9 18. 1 5 6 8 10 / 2 3 4 7 9

8 7
							****
6						****	****
5					****	****	****
4				****	****	****	****
3			****	****	****	****	****
2		****	****	****	****	****	****
	****	****	****	****	****	****	****

1 2 3 4 5 6 7 8

Диаграмма 2. Число игр против каждого из соперников (4 на 4)

Для 66: Rti = Rtсред + 5.5 . (18)

1. 1 2 3 4 9 11 / 5 6 7 8 10 12 7. 1 3 4 5 6 10 / 2 7 8 9 11 12

2. 1 2 3 5 7 8 / 4 6 9 10 11 12 8. 1 4 5 8 9 12 / 2 3 6 7 10 11

3. 1 2 6 8 9 10 / 3 4 5 7 11 12 9. 1 5 7 9 10 11 / 2 3 4 6 8 12

4. 1 2 4 7 10 12 / 3 5 6 8 9 11 10. 1 2 5 6 11 12 / 3 4 7 8 9 10

5. 5. 1 3 6 7 9 12 / 2 4 5 8 10 11 11. 1 4 6 7 8 11 / 2 3 5 9 10 12

6. 1 3 8 10 11 12 / 2 4 5 6 7 9

Для 1010: Rti = Rtсред + 9.5 . (19)

1. 1 2 3 4 5 6 7 8 9 10 / 11 12 13 14 15 16 17 18 19 20

2. 1 2 3 4 5 11 12 13 14 15 / 6 7 8 9 10 16 17 18 19 20

3. 1 2 3 6 8 14 15 16 19 20 / 4 5 7 9 10 11 12 13 17 18

4. 1 2 3 7 9 12 15 17 18 19 / 4 5 6 8 10 11 13 14 16 20

5. 1 2 4 7 8 11 12 16 17 20 / 3 5 6 9 10 13 14 15 18 19

6. 1 2 4 6 10 12 13 18 19 20 / 3 5 7 8 9 11 14 15 16 17

7. 1 2 5 6 9 11 14 17 18 20 / 3 4 7 8 10 12 13 15 16 19

8. 1 2 5 7 10 13 14 16 17 19 / 3 4 6 8 9 11 12 15 18 20

9. 1 2 8 9 10 11 13 15 16 18 / 3 4 5 6 7 12 14 17 19 20

10. 1 3 5 7 8 11 13 18 19 20 / 2 4 6 9 10 12 14 15 16 17

11. 1 3 4 6 9 11 13 16 17 19 / 2 5 7 8 10 12 14 15 18 20

12. 1 3 4 5 10 15 16 17 18 20 / 2 6 7 8 9 11 12 13 14 19

13. 1 3 6 7 10 11 12 14 16 18 / 2 4 5 8 9 13 15 17 19 20

14. 1 3 8 9 10 12 13 14 17 20 / 2 4 5 6 7 11 15 16 18 19

15. 1 4 5 8 9 12 14 16 18 19 / 2 3 6 7 10 11 13 15 17 20

16. 1 4 6 7 8 13 14 15 17 18 / 2 3 5 9 10 11 12 16 19 20

17. 1 4 7 9 10 11 14 15 19 20 / 2 3 5 6 8 12 13 16 17 18

18. 1 5 6 7 9 12 13 15 16 20 / 2 3 4 8 10 11 14 17 18 19

19. 1 5 6 8 10 11 12 15 17 19 / 2 3 4 7 9 13 14 16 18 20

В тексте диссертации приведены также распределения (8 8) и (3 3).

ПЕДАГОГИЧЕСКИЙ ЭКСПЕРИМЕНТ

Формирование рейтинг-листа. Чтобы получить рейтинг-лист, необходимо из рейтингов игроков определить рейтинг команды и совместить его с результатами команд-соперников.

Таблица 2

Сводная таблица 1 этапа Кубка России 1993 г.

Команды	Результаты игр								З:П	Rt
	1	2	3	4	5	6	7	8
Феникс		5:5	6:1	11:0	-	6:2	11:0	-	39:8	3153
Строитель	5:5		5:5	8:1	6:3	-	-	9:3	33:17	2963
Торнадо	1:6	5:5		9:6	7:2	-	-	6:3	28:22	2617
Луч	0:11	1:8	6:9		-	10:5	4:4	-	21:37	2384
Сибиряк	-	3:6	2:7	-		8:4	-	7:1	20:18	2654
Янтарь	2:6	-	-	5:10	4:8		9:2	-	20:26	2432
Корус	0:11	-	-	4:4	-	2:9		4:5	10:29	2137
Мелиус	-	3:9	3:6	-	1:7	-	5:4		12:26	2426

Средний рейтинг команд высшей лиги был принят равным 3000. Из этого, по результатам чемпионата страны, получили рейтинги представителей высшей лиги в кубковом полуфинале – команды «Феникс», «Строитель» и «Сибиряк». На этот момент рейтинги игроков были известны из результатов контрольных игр, исходя из равенства среднего по команде рейтинга 3000 пунктов. Из полученных в контрольных играх рейтингов игроков, пропорционально результативности за время их пребывания на поле в официальном турнире формировали рейтинг команды, который через СЛУ сопоставляли с рейтингами команд-соперников. Так получили два рейтинга «Торнадо», которые совместили за счет одинакового уменьшения рейтингов игроков. Рейтинг команды, исходя из результатов контрольных игр, получается: Rt = 3705. В вышеупомянутом турнире рейтинг команды оказался равным 2620. Рейтинги игроков «Торнадо» были уменьшены на разницу в 3705 - 2620 = 1085. Сводные данные приведены в таблице 2.

Организационно-педагогические условия тренировки, ориентированной на рейтинг-лист. В полученных формулах использованы фиксированные равные коэффициенты i. Поэтому необходимо стремиться к тому, чтобы фактическое распределение нагрузок было как можно ближе к равномерному. Если использовать голевую шкалу рейтинга, то неравная по микроматчам сумма голов нарушает равномерность распределения, что позволяет получить только приблизительное решение или приводит к необходимости решать полученную СЛУ. В рамках настоящей работы контрольные игры проводились, как правило, до двух забитых мячей. После забивания первого мяча команды проводили смену ворот. Это позволяет нивелировать фактор вратаря. Если микротурнир выходит из привычного режима (5 минут - игра, 5 минут - отдых), то в этом случае постепенно сокращали численность обеих сторон. Оценивали средний уровень результатов за последний месяц (6).

С педагогической точки зрения знакомство с личным первенством для игроков должно пройти четыре этапа. На первом этапе игроки убеждаются, что условия соревнования равны для всех и, стало быть, зависят только от их игры. На втором - игрок самостоятельно вычисляет свой рейтинг, что вызывает у него доверие к результатам. На третьем - он убеждается в том, что тренер при подборе состава на официальный турнир руководствуется итогами контрольных игр. На четвертом - он видит результаты своих тренировочных усилий на рейтинг-листе и имеет возможность оценить их эффективность. Необходимо, чтобы у всех участников был достаточно большой психологический стимул совершенствовать свой уровень игры. Рейтинг-лист дает возможность сопоставления своего уровня с уровнем ведущих команд, игроков. Это позволяет перенести ответственность за результативность тренировочного процесса на самого игрока и побуждает его к активному участию в этом. Тренировочные игры малоэффективны из-за постоянно снижающегося к концу сезона уровня противостояния. В контрольных играх это вряд ли возможно. Тренер предлагает воспитанникам самим определить – кто сильнейший. Именно психологическое противостояние внутри коллектива, амбиции и претензии на лидерство, подстегиваемые стимулом попадания в основной состав, не дают опускаться уровню противостояния на низкую отметку. При этом достоверность уровня результатов гарантируется усреднением итогов контрольных игр за последний месяц. Получая эти данные, тренеры точнее определяют состав и распределяют нагрузку.

РЕЗУЛЬТАТЫ ПЕДАГОГИЧЕСКОГО ЭКСПЕРИМЕНТА. Полученные данные были сопоставлены с новыми результатами через два с половиной месяца. Состав команды не изменился.

Таблица 3

Изменение рейтинга игроков «Торнадо» через 2.5 месяца

Игроки	1		2		3		4	5		6		7	8
Rtі исход	2835		2975		2785		2370	2145		2365		2235	2200
і	0.14		0.2		0.16		0.12	0.1		0.08		0.08	0.12
Rtі итогов	3060		2925		2960		2590	2260		2490		2220	2060
Эффект		225		-50	175	220			115	125	-15			-140